Important Ncert examples 10th

 NCERT Examples Class 10th Updated 

                                    Chapter - 1   Real Numbers 

Example 1 : Consider the numbers 4n, where n is a natural number. Check whether there is any value of n for which 4n ends with the digit zero.

Example 2 : Find the LCM and HCF of 6 and 20 by the prime factorisation method.

Example 3: Find the HCF of 96 and 404 by the prime factorisation method. Hence, find their LCM.

Example 4 : Find the HCF and LCM of 6, 72 and 120, using the prime factorisation method.

Example 5 : Prove that √3 is irrational.

Example 6 : Show that 5 – √3 is irrational.

Example 7 : Show that 3√2 is irrational.

    

                              Ch -2     Polynomials 

Example 1 : Look at the graphs in Figure given below. Each is the graph of y = p(x), where p(x) is a polynomial. For each of the graphs, find the number of zeroes of p(x).

Example 2 : Find the zeroes of the quadratic polynomial x² + 7x + 10, and verify the relationship between the zeroes and the coefficients.

Example 3 : Find the zeroes of the polynomial x² – 3 and verify the relationship between the zeroes and the coefficients.

Example 4 : Find a quadratic polynomial, the sum and product of whose zeroes are – 3 and 2, respectively.

                        Chapter - 3         PAIR OF LINEAR EQUATIONS IN TWO VARIABLES

Example 1 : Check graphically whether the pair of equations   x + 3y = 6  and 2x – 3y = 12  is consistent. If so, solve them graphically.

Example 2 : Graphically, find whether the following pair of equations has no solution, unique solution or infinitely many solutions: 5x–8y+1= 0 and 3x – 24 / 5 y + 3/5 = 0

Example 3 : Champa went to a ‘Sale’ to purchase some pants and skirts. When her friends asked her how many of each she had bought, she answered, “The number of skirts is two less than twice the number of pants purchased. Also, the number of skirts is four less than four times the number of pants purchased”. Help her friends to find how many pants and skirts Champa bought.

Example 4 : Solve the following pair of equations by substitution method:   7x – 15y = 2 and  x + 2y = 3 . 

Example 5 : Solve the following question—Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Represent this situation algebraically and graphically by the method of substitution.

Example 6 : In a shop the cost of 2 pencils and 3 erasers is ₹9 and the cost of 4 pencils and 6 erasers is ₹18. Find the cost of each pencil and each eraser.

Example 7 : Two rails are represented by the equations x+2y–4=0 and 2x+4y–12=0. Will the rails cross each other?

Example 8 : The ratio of incomes of two persons is 9 : 7 and the ratio of their expenditures is 4 : 3. If each of them manages to save  ₹2000 per month, find their monthly incomes.

Example 9 : Use elimination method to find all possible solutions of the following pair of linear equations :          2x + 3y = 8             4x + 6y = 7

Example 10 : The sum of a two-digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?

                                             Chapter - 4      QUADRATIC EQUATIONS

Example 1 : Represent the following situations mathematically:

(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.

(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was  ₹750. We would like to find out the number of toys produced on that day.

Example 2 : Check whether the following are quadratic equations:

(i) (x–2)² + 1 = 2x–3                         

(ii) x(x+1) + 8 = (x+2) (x–2)

(iii) x(2x+3)=x² +1 

(iv) (x+2)³ = x³ –4 

 Example 3 : Find the roots of the equation 2x² – 5x + 3 = 0, by factorisation.

Example 4 : Find the roots of the quadratic equation 6x² – x – 2 = 0.

Example 5 : Find the roots of the quadratic equation 3x² - 2√6x + 2 = 0.

Example 6 : Find the dimensions of the prayer hall given below : 

Example 7: Find the discriminant of the quadratic equation 2x² – 4x + 3 = 0, and hence find the nature of its roots.

Example 8 : A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?

Example 9 : Find the discriminant of the equation 3x² – 2x + 1/3 = 0 and hence find the nature of its roots. Find them, if they are real.

                                        chapter - 5  ARITHMETIC PROGRESSIONS

Example1:For the AP: 3/2, 1/2,– 1/2,– 3/2 ,..., write the first term a and the common difference d.

Example 2 : Which of the following list of numbers form an AP? If they form an AP, write the next two terms :

(i) 4,10,16,22,...

(ii) 1,–1,–3,–5,...

(iii) –2,2,–2,2,–2,...

(iv) 1,1,1,2,2,2,3,3,3,...

Example 3 : Find the 10th term of the AP: 2,7,12,...

Example 4 : Which term of the AP : 21,18,15,...is –81?Also,is any term 0 ? Give reason for your answer.

Example 5 : Determine the AP whose 3rd term is 5 and the 7th term is 9.

 Example 6 : Check whether 301 is a term of the list of numbers 5, 11, 17, 23, . . .

Example 7 : How many two-digit numbers are divisible by 3 ? 

Example 8 : Find the 11th term from the last term (towards the first term) of the

AP : 10, 7, 4, . . ., – 62.

Example 9 : A sum of  ₹1000 is invested at 8% simple interest per year. Calculate the interest at the end of each year. Do these interests form an AP? If so, find the interest at the end of 30 years making use of this fact.

Example 10 : In a flower bed, there are 23 rose plants in the first row, 21 in the second, 19 in the third, and so on. There are 5 rose plants in the last row. How many rows are there in the flower bed?

 Example 11 : Find the sum of the first 22 terms of the AP : 8, 3, –2, . . .

 Example 12 : If the sum of the first 14 terms of an AP is 1050 and its first term is 10, find the 20th term.

Example 13 : How many terms of the AP : 24, 21, 18, . . . must be taken so that their sum is 78?

Example 14 : Find the sum of :

(i) the first 1000 positive integers             

(ii) the first n positive integers

Example 15 : Find the sum of first 24 terms of the list of numbers whose nth term is given by  aₙ = 3 + 2n

Example 16 : A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year, find :

(i) the production in the 1st year

(ii) the production in the 10th year 

(iii) the total production in first 7 years

                chapter - 6 TRIANGLES

 Example 1 : If a line intersects sides AB and AC of a  ∆ ABC at D and E respectively and is parallel to BC, prove that AD / AB  = AE / AC 

Example 2 : ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show that AE/ED = BF/FC . 

Example3:In the Figure, PS/SQ = PT/TR and ㄥPST  =  ㄥPRQ. Prove that PQR is an isosceles triangle.

Example 4 : In the figure if PQ || RS, prove that  ΔPOQ ~ Δ SOR.

Example 5 : Observe the figure and then find ㄥP.

Example 6 : In the figure OA . OB = OC . OD. Show that ㄥA = ㄥC and  ㄥB = ㄥD. 

Example 7 : A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.

Example 8 : In the figure, CM and RN are respectively the medians of  Δ ABC and  Δ PQR. If Δ ABC ~ Δ PQR, prove that :

(i) Δ AMC ~ Δ PNR

 (ii) CM/RN = AB/PQ

(iii) Δ CMB ~ Δ RNQ

            

                                               chapter - 7  COORDINATE GEOMETRY

Example 1 : Do the points (3, 2), (–2, –3) and (2, 3) form a triangle? If so, name the type of triangle formed.

Example 2 : Show that the points (1, 7), (4, 2), (–1, –1) and (– 4, 4) are the vertices of a square.

Example 3 : In the figure, shows the arrangement of desks in a classroom. Ashima, Bharti and Camella are seated at A(3, 1), B(6, 4) and C(8, 6) respectively. Do you think they are seated in a line? Give reasons for your answer.

Example 4 : Find a relation between x and y such that the point (x , y) is equidistant from the points (7, 1) and (3, 5).

Example 5 : Find a point on the y-axis which is equidistant from the points A(6, 5) and B(– 4, 3).

Example 6 : Find the coordinates of the point which divides the line segment joining the points (4, – 3) and (8, 5) in the ratio 3 : 1 internally.

Example 7 : In what ratio does the point (– 4, 6) divide the line segment joining the points A(– 6, 10) and B(3, – 8) ?

Example 8 : Find the coordinates of the points of trisection (i.e., points dividing in three equal parts) of the line segment joining the points A(2, – 2) and B(– 7, 4).

Example 9 : Find the ratio in which the y-axis divides the line segment joining the points (5, – 6) and (–1, – 4). Also find the point of intersection.

Example 10 : If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.

                                    Chapter - 8     INTRODUCTION TO TRIGONOMETRY

Example 1 : Given tan A = 4/3 , find the other trigonometric ratios of the angle A.

Example 2 : If  ㄥB and ㄥQ are acute angles such that sin B = sin Q, then prove that ㄥB = ㄥQ.

Example 3 : Consider Δ ACB, right-angled at C, in which AB = 29 units, BC = 21 units and  ㄥABC = θ (in the figure). Determine the values of

(i) cos² θ + sin² θ, 

(ii) cos² θ – sin² θ. 

Example 4 : In a right triangle ABC, right-angled at B, if tan A = 1, then verify that

2 sinAcosA = 1.

Example 5 : In  Δ OPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm (in the figure). Determine the values of sin Q and cos Q.

Example 6 : In Δ ABC, right-angled at B, AB = 5 cm and ㄥACB = 30° (in the figure). Determine the lengths of the sides BC and AC.

Example 7 : In ∆ PQR, right-angled at Q (in the figure), PQ = 3 cm and PR = 6 cm. Determine ㄥ QPR and ㄥ PRQ.

Example 8 : If sin (A–B) = 1/2, cos (A+B) = 1/2, 0° < A+B ≤ 90°, A>B, find A and B.

Example 9 : Express the ratios cos A, tan A and sec A in terms of sin A.

Example 10 : Prove that sec A (1 – sin A)(sec A + tan A) = 1.

Example 11 : Prove that (cot A – cos A) / (cot A + cos A) = (cosec A - 1 ) / (cosec A + 1) 

 

Example 12 : Prove that  ( sin θ - cos θ + 1) / ( sin θ + cos θ - 1 ) = 1 / ( sec θ - tan θ ) , using the identity sec² θ = 1 + tan² θ. 

                             chapter - 9          SOME APPLICATIONS OF TRIGONOMETRY

( Heights and Distances ) 

Example 1 : A tower stands vertically on the ground. From a point on the ground, which is 15 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.

Example 2 : An electrician has to repair an electric fault on a pole of height 5 m. She needs to reach a point 1.3m below the top of the pole to undertake the repair work (in the figure). What should be the length of the ladder that she should use which, when inclined at an angle of 60° to the horizontal, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder? (You may take √3 = 1.73)

Example 3 : An observer 1.5 m tall is 28.5 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney? 

 Example 4 : From a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45°. Find the length of the flagstaff and the distance of the building from the point P. (You may take √3 = 1.732)

Example 5 : The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.

Example 6 : The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building and the distance between the two buildings.

Example 7 : From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.

                        chapter - 10  CIRCLES 

Example 1 : Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.

Example 2 : Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ㄥPTQ = 2 ㄥOPQ.

Example 3 : PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (in the figure). Find the length TP.

                         chapter - 11   AREAS RELATED TO CIRCLES

Example 1 : Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14).

Example 2 : Find the area of the segment AYB (in the figure), if radius of the circle is 21 cm and

ㄥAOB = 120°. (Use π = 22/7 )

                                chapter - 12  SURFACE AREAS AND VOLUMES

Example 1 : Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere (in the figure). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = 22/7 )

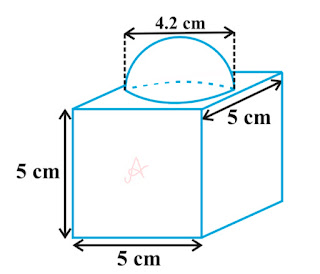
Example 2 : The decorative block shown in the figure is made of two solids — a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block.

(Take π = 22/7 )

Example 3 : A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in figure. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14)

Example 4 : Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end (in the figure). The height of the cylinder is 1.45 m and its radius is 30 cm. Find the

total surface area of the bird-bath. (Take π = 22/7 )

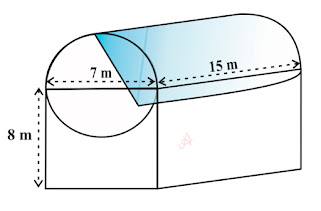
Example 5 : Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder (in the figure). If the base of the shed is of dimension 7 m × 15 m, and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold. Further, suppose the machinery in the shed occupies a total space of 300 m³, and there are 20 workers, each of whom occupy about 0.08 m³ space on an average. Then, how much air is in the shed? (Take π = 22/7 )

Example 6 : A juice seller was serving his customers using glasses as shown in the figure. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity. (Use π = 3.14.)

Example 7 : A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)

                       chapter - 13      STATISTICS

     

Example 1 : The marks obtained by 30 students of Class X of a certain school in a Mathematics paper consisting of 100 marks are presented in table below. Find the mean of the marks obtained by the students.

Example 2 : The table below gives the percentage distribution of female teachers in the primary schools of rural areas of various states and union territories (U.T.) of India. Find the mean percentage of female teachers by all the three methods discussed in this section.

Example 3 : The distribution below shows the number of wickets taken by bowlers in one-day cricket matches. Find the mean number of wickets by choosing a suitable method. What does the mean signify?

Example 4 : The wickets taken by a bowler in 10 cricket matches are as follows: 

                       2        6        4        5        0        2        1        3        2        3

Find the mode of the data.

Example 5 : A survey conducted on 20 households in a locality by a group of students resulted in the following frequency table for the number of family members in a household:

Find the mode of this data. 

Example 6 : A survey regarding the heights (in cm) of 51 girls of Class X of a school was conducted and the following data was obtained:

Find the median height. 

Example 7 : The median of the following data is 525. Find the values of x and y, if the total frequency is 100.

                             Chapter - 14    PROBABILITY 

Example 1 : Find the probability of getting a head when a coin is tossed once. Also find the probability of getting a tail.

Example 2 : A bag contains a red ball, a blue ball and a yellow ball, all the balls being of the same size. Kritika takes out a ball from the bag without looking into it. What is the probability that she takes out the

(i) yellow ball?                                             (ii) red ball?                                                  (iii) blue ball?

Example 3 : Suppose we throw a die once. (i) What is the probability of getting a number greater than 4 ? (ii) What is the probability of getting a number less than or equal to 4 ?

Example 4 : One card is drawn from a well-shuffled deck of 52 cards. Calculate the probability that the card will

(i) be an ace,

(ii) not be an ace.

Example 5 : Two players, Sangeeta and Reshma, play a tennis match. It is known that the probability of Sangeeta winning the match is 0.62. What is the probability of Reshma winning the match?

Example 6 : Savita and Hamida are friends. What is the probability that both will have (i) different birthdays? (ii) the same birthday? (ignoring a leap year).

Example 7 : There are 40 students in Class X of a school of whom 25 are girls and 15 are boys. The class teacher has to select one student as a class representative. She writes the name of each student on a separate card, the cards being identical. Then she puts cards in a bag and stirs them thoroughly. She then draws one card from the bag. What is the probability that the name written on the card is the name of (i) a girl? (ii) a boy?

Example 8 : A box contains 3 blue, 2 white, and 4 red marbles. If a marble is drawn

at random from the box, what is the probability that it will be

 (i) white?                                                   (ii) blue?                                     (iii) red?

Example 9 : Harpreet tosses two different coins simultaneously (say, one is of ₹ 1 and other of ₹ 2). What is the probability that she gets at least one head?

Example 10 : A carton consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Jimmy, a trader, will only accept the shirts which are good, but Sujatha, another trader, will only reject the shirts which have major defects. One shirt is drawn at random from the carton. What is the probability that

(i) it is acceptable to Jimmy?                                             (ii) it is acceptable to Sujatha?

Example 11 : Two dice, one blue and one grey, are thrown at the same time. Write down all the possible outcomes. What is the probability that the sum of the two numbers appearing on the top of the dice is

(i) 8?                                         (ii) 13?                                          (iii) less than or equal to 12?

Do practice well. 

Solutions - coming soon 

Thanks for visiting.